Kerckhoffs’sPrinciple(柯克霍夫法则)
一个密码体制即使除密钥外的所有细节都公开,也应保持安全。强调“敌人了解系统”这一前提。
Classical Ciphers(古典密码)
Substitution cipher(替换密码)
逐字母替换明文 (Substitute letters of plaintext one by one)。例如:凯撒密码 (Caesar Cipher)、维吉尼亚密码 (Vigenere)、Hill
Transposition cipher(置换密码)
明文的字符分组移动位置 (The positions held by groups of characters of plaintext are shifted)
Symmetric Encryption(对称加密)
流密码 (Stream Cipher)
一次一密体制 (One-Time Pad Scheme):理论上无条件安全。
加密:$𝑦_𝑖 = 𝑥_𝑖 \bigoplus 𝑠_𝑖$
解密:$𝑥_𝑖 = 𝑦_𝑖 \bigoplus 𝑠_𝑖$
要求:密文、明文、密钥等长 (𝑦, 𝑥, 𝑠 are of the same size),且密钥 $s$ 必须是随机的,$n$ -bit 密钥有 $2^n$ 可能的值 (Key $s$ is random, n-bit key has $2^n$ possible values)
流密码 (Stream Cipher):是对一次一密体制的模拟,核心是密钥流生成器 (The simulation of One-Time Pad Scheme, the kernel is keystream generator)
线性反馈移位寄存器 (LFSR):一种常见的密钥流生成器。Linear Feedback Shift Register
LFSR是根据线性反馈函数 f(x1,x2,…,xn) 和初始值来生成序列或密钥流的(通过一个预定义的线性关系和一组起始状态来迭代生成输出序列)
LFSR的数学基础是可以通过多项式来描述的(Polynomial representation of f(x1,x2,…,xn ))
m-序列(m-sequence)是由LFSR生成的一类重要的伪随机序列,具有优良的统计特性
Modern Stream Cipher: RC4, Trivium, ZUC which have nonlinear parts(非线性部件)
分组密码(Block Cipher)
设计原则 (Design Principles):混淆 (Confusion) 和扩散 (Diffusion)。
与流密码的区别:
-
分组密码:逐块加密明文 (Encrypt the plaintext block-by-block)。
-
流密码:逐比特加密明文 (Encrypt the plaintext bit-by-bit)。
常见分组密码 (Common Block Cipher):
-
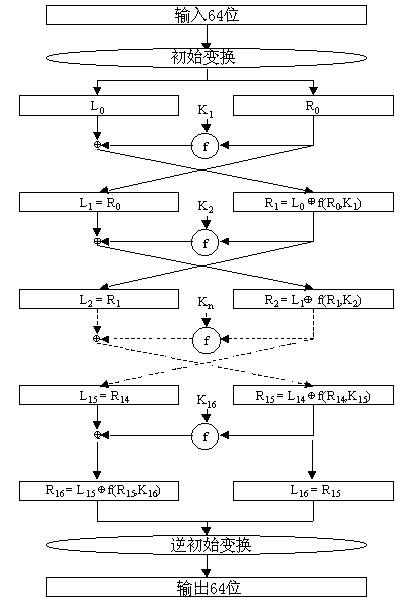
DES (数据加密标准) 和 3DES:DES 的分组长度为 64 位,密钥长度为 56 位。
-
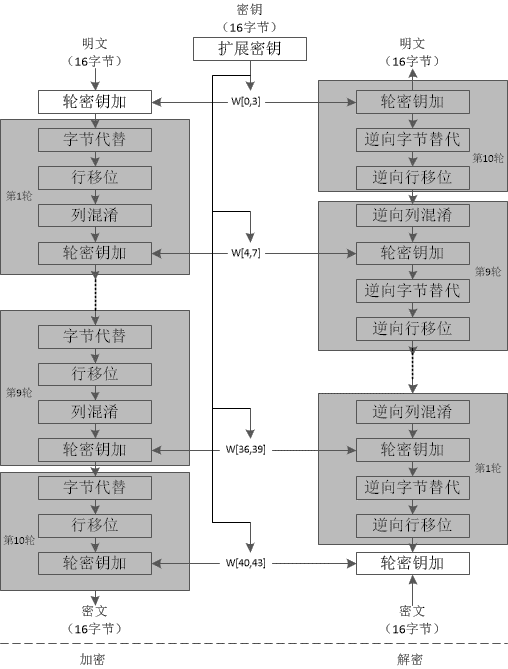
AES (高级加密标准):
-
SM4(国密)
Operation Modes of Block Cipher(分组密码操作模式)
提高分组密码安全性
-
多重加密 (Multiple encryption):理论上更安全,但实际中安全提升有限。
-
密钥漂白 (Key whitening)。
-
中间相遇攻击 (Meet-in-the-Middle Attack):
-
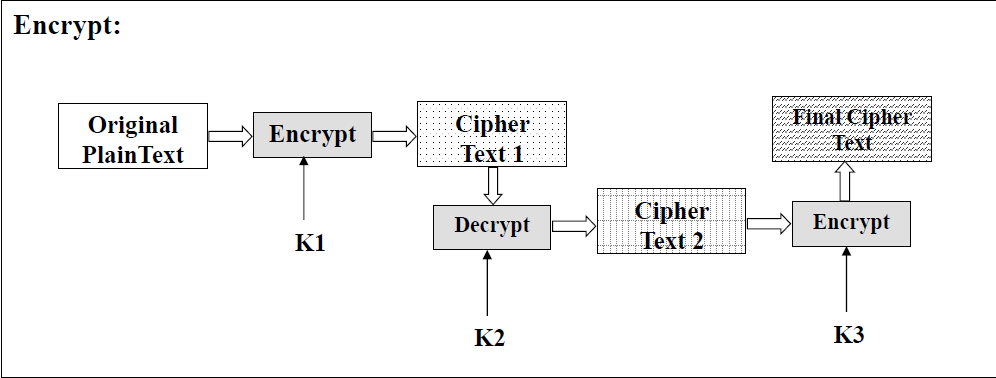
三重 DES (Triple DES):
-
加密:$y = DES_{K3}(DES^{-1}_{K2}(DES_K1(x)))$。
-
解密:$x = DES^{-1}K1(DES_{K2}(DES^{-1}_K3(y)))$。
-
优势:显著提高安全性,对抗中间相遇攻击的能力增强,提供更长的有效密钥长度,增加非线性变换。
-
相较于双重DES的优势:
-
增加的安全性:三重DES通过三次使用DES算法来加密数据,显著增加了安全性,这比单一DES加密要强得多。多轮加密和解密使得攻击者更难通过暴力破解方法破解加密。
-
抵抗中间相遇攻击:这是三重DES被设计出来主要解决的问题。双重DES易受中间相遇攻击的影响,这会降低其有效密钥长度。三重DES,尤其是在使用三个不同密钥的情况下,对这类攻击的抵抗力要强得多,因为攻击的复杂性会随着每一层额外的加密呈指数级增长。例如,对于使用三个不同密钥的三重DES,中间相遇攻击的复杂度接近 $2^{2K}$,而不是 $2^{K+1}$,这大大提高了其安全性。
-
有效密钥长度:三重DES可以提供更长的有效密钥长度。虽然双重DES理论上具有112比特的密钥长度,但由于中间相遇攻击的漏洞,它并未实现完整的安全效益,有效安全性降低到小于单个DES的两倍。三重DES在实践中能够达到112比特甚至更高的有效安全性(取决于密钥的使用方式)
-
增加非线性变换:多次加密增加了更多的非线性变换。这使得攻击者更难利用线性密码分析和差分密码分析技术来破解加密。
-
兼容性和灵活性
-
-
分组密码操作模式 (Operation Modes of Block Cipher)
- ECB Mode (Electronic Code Book, 电子密码本模式)
- CBC Mode (Ciphertext Block Chaining, 密文分组链接模式)
- CFB Mode (Ciphertext Feedback, 密文反馈模式)
- OFB Mode (Output Feedback, 输出反馈模式)
- CTR Mode (Counter, 计数器模式)
- GCM (Galois Counter Mode 伽罗瓦计数器模式)
Public-Key Encryption(公钥加密)
思想 (Idea of Public-key Encryption):
- Diffie 和 Hellman 提出,将密钥分为公钥和私钥,公钥用于加密,私钥用于解密。
- 任何人都可以加密,只有私钥拥有者可以解密。
- 加密是容易的,解密是困难的(除非拥有私钥)。
- 加密是“单向(One-Way)”行为,带陷门(私钥private key)的单向函数。
数学基础 (Math Foundation):基于数学中的“难题”(Hard Problems behind Public-Key Cryptography)。
- 整数分解 (Factorization):给定 $N = p \cdot q$,分解得到大素数 $p$ 和 $q$。
- 离散对数 (Discrete Logarithm):给定 $y = g^x \pmod p$,计算 $x$。
- 椭圆曲线离散对数 (Elliptic Curve Discrete Logarithm):给定 $P = d \cdot G$,计算 $d$。
重要数学工具:
- 欧几里得算法
- 计算两个整数的最大公约数 (gcd) 即辗转相除法
- 扩展欧几里得算法 (EEA):计算出整数 $s$ 和 $t$,使得 $sa + tb = gcd(a, b)$
- 模算术和欧拉函数
- 在模 $p$ 的整数集合 $\mathbb{Z}_p$ (其中 $p$ 是素数) 中,$\mathbb{Z}_p$ 包含 ${0, 1, 2, \dots, p-1}$ 这些元素。在 $\mathbb{Z}_p$ 上可以定义加法、减法、乘法,以及除法(求逆+乘法)
- 欧拉函数 $\phi(n)$ 计算的是小于或等于 $n$ 且与 $n$ 互素的正整数的个数。
- 对于素数 $p$,欧拉函数 $\phi(p) = p-1$
- 对于素数幂 $p^t$,欧拉函数 $\phi(p^t) = p^t - p^{t-1}$
- 对于一个可以分解为多个素数幂乘积的整数 $n = p_1^{t_1} \cdot \dots \cdot p_s^{t_s}$,其欧拉函数 $\phi(n)$ 可以通过以下公式计算: $$ \phi(n) = \prod_{i=1}^{s} (p_i^{t_i} - p_i^{t_i-1}) $$
- 费马小定理
- 对于一个素数 $p$ 和任意整数 $a$,有 $a^p \equiv a \pmod{p}$
- 欧拉定理
- 对于整数 $a$ 和 $m$,如果它们互素(即 $\text{gcd}(a, m) = 1$),那么 $a^{\phi(m)} \equiv 1 \pmod{m}$
RSA 加密体制 (RSA Cryptosystem)
密钥生成 (Key Generation):
-
选择两个大素数(k-bit primes) $p, q$。$k= 512, 1024, 2048…$
-
使用Miller-Rabin素性检测(Miller-Rabin Primality Test)随机选取p,q
-
计算 $n = p \cdot q$。
-
计算欧拉函数 $\varphi(n) = (p-1)(q-1)$。
-
选择 $e$ 使得 $gcd(e, \varphi(n)) = 1$。
-
计算 $d = e^{-1} \pmod{\varphi(n)}$。
-
公开参数:$n$;公钥:$e$;私钥:$d$。
加密 (Encryption):$y = e_{k_{pub}}(x) \equiv x^e \pmod n$。
解密 (Decryption):$x = d_{k_{pr}}(y) \equiv y^d \pmod n$。
加速技术:
- 平方乘算法 (Square-and-Multiply algorithm)
- 短公开指数快速加密 (Fast Encryption with Short Public Exponents)
- 转换输入到 CRT 域 (Transformation of the Input into the CRT Domain)
Elgamal 加密体制 (Elgamal Cryptosystem)
密钥生成 (Key Generation):
-
选择大素数 $p$ 和模 $p$ 的本原元 $g$。
-
随机选择私钥 $x \in (1, p-1)$。
-
计算公钥 $y = g^x \pmod p$。
加密 (Encryption):
- 对消息 $m \in [0, p-1]$,随机选择 $k \in [1, p-2]$。
- 计算 $u = g^k \pmod p$, $v = m \cdot y^k \pmod p$。
- 密文为 $c = (u, v)$ by $p, g ,y$
解密 (Decryption):使用私钥 $x$,恢复 $m = u^{p-1-x} \cdot v \pmod p$
Elgamal: Example :
公共参数:$p = 17$ (一个大素数) $g = 3$ (模 $p$ 的本原元)
- 密钥生成:随机选择 $x = 14$,作为私钥。
- 计算 $y = g^x \pmod{p} = 3^{14} \pmod{17} = 2$,作为公钥。
加密 (Enc):明文 $m = 10$。
- 随机选择 $k = 12$。
- 计算 $u = g^k \pmod{p} = 3^{12} \pmod{17} = 4$。
- 计算 $v = m \cdot y^k \pmod{p} = 10 \cdot 2^{12} \pmod{17} = 7$。
- 密文 $c = (u, v) = (4, 7)$。
解密 (Dec):使用私钥 $x = 14$。
- 恢复明文 $$m = u^{p-1-x} \cdot v \pmod{p} = 4^{17-1-14} \cdot 7 \pmod{17} = 10$$
Diffie-Hellman 密钥交换 (DH Key Exchange)
目标:爱丽丝和鲍勃在不安全的信道上协商一个共享密钥(same key)。
原理:利用 $(g^a)^b \pmod p = (g^b)^a \pmod p = g^{ab} \pmod p$。
安全性:基于**离散对数(Discrete Logarithm)**难题的困难性。
Example :
- 公共参数:
- $p = 17$
- $g = 3$
- Alice的操作:
- Alice选择私钥 $a = 10$。
- Alice计算 $g^a \pmod{17} = 3^{10} \pmod{17} = 8$。
- Alice将计算结果 $8$ 发送给Bob。
- Bob的操作:
- Bob选择私钥 $b = 11$。
- Bob计算 $g^b \pmod{17} = 3^{11} \pmod{17} = 7$。
- Bob将计算结果 $7$ 发送给Alice。
- 共同密钥的计算:
- Alice计算 $({g^b})^a \pmod{17} = 7^{10} \pmod{17} = 2$。
- Bob计算 $({g^a})^b \pmod{17} = 8^{11} \pmod{17} = 2$。
- 因此,Alice和Bob协商得到相同的密钥 $2$。
所有这些运算都在模 $p$ 下进行。敌手虽然知道 $p, g, g^a, g^b$,但无法计算出 $g^{ab}$。
椭圆曲线密码体制 (Elliptic Curve Cryptosystem, ECC)
基础:基于椭圆曲线上的点加运算。
公共参数:通常使用公开标准化文档中给定的参数,包括素数 $p$、椭圆曲线方程系数 $a, b$、基点 $G$。
私钥$d$ , 公钥$P= d∙G$
在椭圆曲线群中,给定 $G$ 和 $d$,计算 $P$ 是容易的;但反过来,已知 $P$ 和 $G$,却很难计算出 $d$
这就是椭圆曲线离散对数难题3。这是ECC安全性的基石。
ECDHKE (Elliptic Curve Diffie-Hellman Key Exchange):椭圆曲线版本的 DH 密钥交换,安全性基于椭圆曲线离散对数难题。
公共参数 :
- 一个大素数 $p$。
- 一条椭圆曲线 $E$,其方程通常表示为 $y^2 \equiv x^3+a \cdot x+b \pmod p$,其中 $a$ 和 $b$ 是曲线的系数。
- 一个椭圆曲线上的基点 $P = (x_P, y_P)$,也被称为原语元素 (primitive element)。
密钥交换过程 :
Alice 和 Bob 通过 ECDHKE 协议来协商一个共同的秘密密钥 $T_{AB}$:
- Alice 的操作:
- Alice 随机选择一个私钥 $k_{prA} = a$,其中 $a$ 是一个整数,且 $a \in {2,3,…, #E-1 }$。
- Alice 计算她对应的公钥 $k_{pubA} = aP = A = (x_A, y_A)$。
- Bob 的操作:
- Bob 随机选择一个私钥 $k_{prB} = b$,其中 $b$ 是一个整数,且 $b \in {2,3,…, #E-1 }$。
- Bob 计算他对应的公钥 $k_{pubB} = bP = B = (x_B, y_B)$。
- 公钥交换:Alice 将她的公钥 $A$ 发送给 Bob,Bob 将他的公钥 $B$ 发送给 Alice。
- 计算共享密钥:
- Alice 接收到 Bob 的公钥 $B$ 后,计算共享密钥 $aB = T_{AB}$。
- Bob 接收到 Alice 的公钥 $A$ 后,计算共享密钥 $bA = T_{AB}$。
由于椭圆曲线上的点乘运算具有结合律,即 $a(bP) = (ab)P$ 和 $b(aP) = (ba)P$ (此特性与DH密钥交换的原理类似),因此 Alice 计算的 $aB$ 等于 Bob 计算的 $bA$,双方最终得到相同的共享密钥 $T_{AB} = (x_{AB}, y_{AB})$。
数字签名 (Digital Signature)
与公钥加密的区别和联系:
- 两者都使用密钥对 (public key, secret key)。
- 公钥加密:确保数据机密性 (data confidentiality)。使用公钥加密,私钥解密。
- 数字签名:确保数据完整性 (data integrity)、消息验证 (Message authentication) 和不可否认性 (non-repudiation)。使用私钥签名,公钥验证。
公钥加密安全性: 无法恢复密钥或消息
数字签名安全性:不能伪造 (forge) 有效签名(valid signature)。
常见数字签名方案:
RSA Signature(RSA签名)
- 密钥生成 (Key Generation):
- 生成两个大素数 $p$ 和 $q$。
- 计算公共参数 $n = p \cdot q$。
- 计算欧拉函数 $\phi(n) = (p-1)(q-1)$。
- 选择一个整数 $e$ 作为公钥,满足 $\text{gcd}(e, \phi(n)) = 1$。
- 计算 $d$ 作为私钥,满足 $ed \equiv 1 \pmod{\phi(n)}$,即 $d = e^{-1} \pmod{\phi(n)}$。
- 因此,公钥为 $(n, e)$,私钥为 $d$。
- 签名 (Signing):
- 给定消息 $m$,签名者使用私钥 $d$ 对消息 $m$ 进行签名,得到签名 $s$。
- 通常,签名的计算方式为 $s = m^d \pmod n$
- 将签名 $s$ 添加到消息 $m$ 后得到 $(m||s)$。
- 在实际应用中,通常是对消息的哈希值进行签名,而不是直接对整个消息进行签名,以解决大数据处理和提高效率的问题。
- 验证 (Verifying):
- 接收者收到 $(m||s)$ 后,使用公共参数 $n$ 和公钥 $e$ 计算 $m' = s^e \pmod n$。
- 如果计算出的 $m' = m$ (或者更准确地说,如果对哈希值签名,则 $m'$ 等于原始消息的哈希值),则验证通过。否则,验证失败。
Elgamal 签名 (Elgamal Signature)
-
公共参数 (Public Parameters):
- 一个大素数 $p$。
- 一个模 $p$ 的本原元 (primitive element) $g$。
-
密钥生成 (Key Generation):
- 私钥 $x$ 是在 $(1, p-1)$ 之间随机选择的整数。
- 公钥 $y = g^x \pmod p$。
-
签名 (Signing):
- 签名者使用公共参数 $p, g$ 和私钥 $x$ 对消息 $m$ 进行签名,得到签名 $(r, s)$。
- 关于密钥的重用问题:在 Elgamal 签名方案中,如果用于生成签名的临时密钥 (ephemeral key) 被重复使用,可能会导致安全问题。
-
验证 (Verifying):
- 接收者使用公钥 $y$ 验证消息 $m$ 和签名 $(r, s)$。
- 验证结果为“通过 (Pass)”或“不通过 (No)”。
-
安全性:临时密钥的重复使用 (Reuse of the Ephemeral Key)
DSA (数字签名算法)
- 公共参数 (Public Parameters):
- 一个大素数 $p$。
- 一个大素数 $q$,且 $q \ll p$。
- 一个元素 $g$,满足 $g$ 是模 $p$ 的 $q$ 阶元 ($\text{ord}_p(g) = q$)。
- 密钥生成 (Key Generation):
- 公钥为 $y$,私钥为 $x$。
- 签名 (Signing):
- 签名者使用公共参数 $p, g$ 和私钥 $x$ 对消息 $m$ 进行签名,得到签名 $(r, s)$。
- 验证 (Verifying):
- 接收者使用公钥 $y$ 验证消息 $m$ 和签名 $(r, s)$。
- 验证结果为“通过 (Pass)”或“不通过 (No)”。
ECDSA(椭圆曲线数字签名)
ECDSA 是 DSA 的椭圆曲线版本。
Elliptic Curve + DSA
Hash函数 (Hash Function)
定义 (Definition):Hash function is a function mapping any message of any length to value of fixed length (任意长度映射至固定长度输出)。
单向性 / 抗第一原像性 (One-wayness):给定输出 $y$,计算得到输入 $x$ 是不可行的(feasible)。
弱抗碰撞性 / 抗第二原像性 (Weak Collision-Resistance):给定 $x$ 和 $h(x)$,找到另一个 $x'$ 使得 $h(x') = h(x)$ 是不可行的。
强抗碰撞性 (Strong Collision-Resistance):找到不同的 $x$ 和 $x'$ 使得 $h(x) = h(x')$ 是不可行的。
常见散列函数:
- MD5, SHA-1 (已不够安全)。
- SHA-2, SHA-3, SM3 (推荐使用)。
应用 (Applications):网站安全登录、检测文件篡改、数字签名等。
生日攻击 (Birthday Attack)
对于一个输出长度为 $n$ 比特的哈希函数,如果随机选择消息进行哈希计算,找到两个不同的输入 $x$ 和 $x'$,使得它们的哈希值相同(即 $h(x) = h(x')$),通常需要大约 $2^{n/2}$ 次哈希计算。
这个 $2^{n/2}$ 的值远小于达到 $2^n + 1$ 次计算必然发生碰撞所需的次数。这种通过相对较少的操作找到碰撞的攻击方式被称为生日攻击。
哈希函数的输出长度是其安全性的关键因素之一。
例如,MD5 的输出长度为 128 比特,SHA-1 的输出长度为 160 比特。
根据生日攻击的原理,对 MD5 进行生日攻击大约需要 $2^{128/2} = 2^{64}$ 次哈希计算来找到碰撞。
对 SHA-1 进行生日攻击大约需要 $2^{160/2} = 2^{80}$ 次哈希计算来找到碰撞。
散列函数在数字签名中的应用
解决大数据处理问题:将大消息哈希成固定大小的摘要 (digest),再对摘要进行签名,提高效率。
提供完整性和认证:消息的任何改变都会导致哈希值不同,接收方通过比较哈希值验证消息的完整性和来源。
提供不可否认性:发送方用私钥对消息的哈希值签名,由于私钥的唯一性,发送方无法否认其签名行为。
消息认证码 (MAC)
目的:确保数据完整性 (data Integrity) 和消息认证 (Message authentication)。
特点:
- 密码学校验和 (Cryptographic checksum):生成密码学安全的验证标签。
- 对称性 (Symmetric):基于共享的对称密钥。
- 任意消息大小 (Arbitrary message size)。
- 固定输出长度 (Fixed output length)。
- 提供消息完整性 (Message integrity):传输过程中对消息的任何操作都将被接收方检测到。
- 消息认证 (Message authentication):接收方确定消息来源。
- 不具有不可否认性 (No nonrepudiation):因为发送方和接收方共享同一密钥,无法证明是哪一方生成的 MAC。
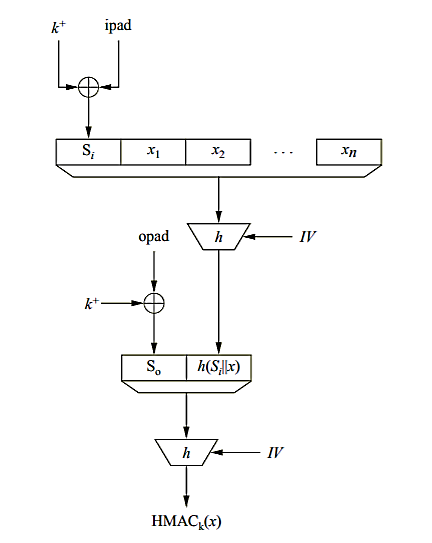
HMAC (基于哈希函数的消息认证码):
利用哈希函数构造,例如:$HMAC_k(x) = h [ (k^+ \oplus opad) || h [ (k^+ \oplus ipad ) || x ] ]$。
k+代表将密钥k填充到哈希函数分组大小后的结果。ipad是重复的0x36值。opad是重复的0x5C值。
应用于 SSL/TLS 等标准。
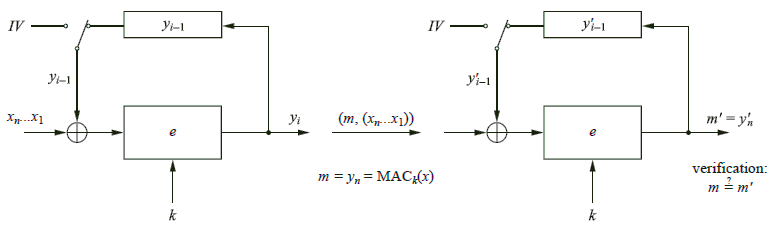
基于分组密码的 MAC (MACs from block ciphers)
消息认证码 (MAC) 由分组密码构建
通常使用 AES 在 CBC 模式下构建
密钥建立 (Key Establishment)
对称密钥建立 (Symmetric Key Establishment):
- 密钥传输 (Key Transport):一方生成密钥并安全地传输给另一方。
- 密钥协商 (Key Agreement):双方共同参与,协商出共享密钥。
密钥刷新 (Key Freshness):
- 在密码系统中,频繁更换密钥通常是可取的
- 通过衍生新的会话密钥来频繁更换密钥,例如 $k_{ses} = HMAC_{k_{AB}}(r)$ 或 $k_{ses} = e_{k_{AB}}(r)$。
$n^2$ 密钥分配问题:随着用户数量增加,所需密钥对呈平方增长。
密钥分配中心 (Key Distribution Center, KDC):
- 一个集中管理和分配密钥的实体,例如 Kerberos 系统。
对称密钥分配的遗留问题
- 通信瓶颈 (Communication bottleneck):KDC 参与网络中每一次通信。
- 初始化时的安全信道要求 (Secure channel during initialization):新用户加入时需要安全信道传输其密钥加密密钥。
- 单点故障 (Single point of failure):KDC 存储所有密钥,一旦泄露,所有历史通信都可能被解密。
- 不提供完美前向保密性 (No Perfect Forward Secrecy, PFS):如果 KDC 的密钥泄露,攻击者可以解密未来的通信,甚至解密存储的历史通信。
中间人攻击 (Man-in-the-Middle Attack)
攻击原理:
- 中间人攻击的核心在于攻击者在通信双方之间建立连接,并对双方都伪装成对方。例如,在 Diffie-Hellman 密钥交换等协议中,攻击者 Oscar 能够计算出与 Alice 的会话密钥 $k_{AO}$ 以及与 Bob 的会话密钥 $k_{BO}$。
- 然而,Alice 和 Bob 却错误地认为他们正在彼此通信。
- 这种攻击通过 Oscar 有效地执行两次 Diffie-Hellman 密钥交换来实现:一次是 Oscar 与 Alice 之间,另一次是 Oscar 与 Bob 之间。
Alice 和 Oscar 共享一个密钥 $k_{AO} = \alpha^{aO} \pmod p$。
Bob 和 Oscar 共享一个密钥 $k_{BO} = \alpha^{bO} \pmod p$。
Alice 认为她与 Bob 建立了共享密钥 $k_{AO}$,Bob 认为他与 Alice 建立了共享密钥 $k_{BO}$。
由于 Oscar 同时拥有这两个会话密钥,他可以解密 Alice 发送给 Bob 的消息(使用 $k_{AO}$),阅读后用 $k_{BO}$ 重新加密发送给 Bob;反之亦然。这使得攻击者可以完全控制并监听双方的所有通信,甚至可以修改消息内容而不会被察觉。
为了解决中间人攻击等问题,通常会引入公钥基础设施 (Public Key Infrastructure, PKI) 和数字证书 (Certificates)。
公钥基础设施 (Public Key Infrastructure, PKI) 和数字证书 (Certificates)
-
解决 DH 密钥交换中的中间人攻击问题。
-
证书机构 (CA):PKI 的核心,负责签发和管理数字证书。
-
数字证书:将用户的身份与公钥一一对应。
-
证书标准:X.509。
PKI 和数字证书如何解决中间人攻击:
- 当 Alice 想要与 Bob 通信时,Bob 不会直接发送他的公钥。
- Bob 会向 Alice 发送他的数字证书,该证书包含了 Bob 的公钥以及由 CA 对该公钥的签名。
- Alice 收到 Bob 的证书后,会使用她预先信任的 CA 的公开密钥来验证 Bob 证书的签名。
- 如果验证成功,Alice 就能够确信证书中的公钥确实是 Bob 的,并且未被篡改。
- 这样,即使中间人 Oscar 试图拦截并用自己的公钥替换 Bob 的公钥,Alice 也能通过验证证书发现这一欺骗,因为 Oscar 的公钥不会有被信任的 CA 签发的有效证书(除非攻击者能攻陷 CA)。
通过验证数字证书,通信方可以确认对方公钥的真实性,从而防止中间人攻击。
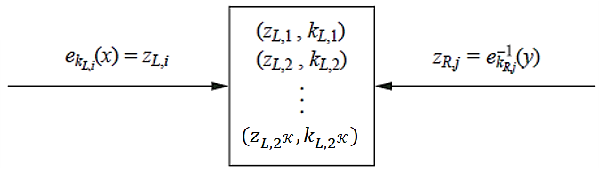

 微信
微信